MECÂNICA GRACELI GENERALIZADA - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [1.251]

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS.

MECÃNICA GRACELI GERAL - QTDRC.

$equação Graceli dimensional relativista tensorial quântica de campos$

$\psi ^{*}$

$[$ $\psi ^{*}$ $G$ * $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $T_{\mu \nu }$ $/$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ +

$+$ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ] $\lambda$ ω ${\mathcal {T}}$ , $\sigma$ , $\psi$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ [x,t] ] =

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES DE CAMPOS E ENERGIAS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

/ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE INTERAÇÕES DE CAMPOS. EM ;

MECÂNICA GRACELI REPRESENTADA POR TRANSFORMADA.

dd = dd [G] = DERIVADA DE DIMENSÕES DE GRACELI.

- [ $G*$ $\hbar$ $.$ $\psi$

G { f [dd]} ´[d] $\psi ^{*}$ $\hbar$ $\psi$ $f [d] G*$ $T_{\mu \nu }$ $\psi$ $dd [G]$

O ESTADO QUÂNTICO DE GRACELI

- [ $G*$ $\hbar$ $.$ $\psi$ $\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigg )},$ ]

$G* = DIMENSÕES DE GRACELI TAMBÉM ESTÁ RELACIONADO COM INTERAÇÕES DE ENERGIAS, QUÂNTICAS, RELATIVÍSTICAS, , E INTERAÇÕES DE CAMPOS.$

o tensor energia-momento $T_{\mu \nu }$ é aquele de um campo eletromagnético,

/ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

A hipótese de De Broglie

Em 1924, Louis-Victor de Broglie formulou a hipótese de Broglie, alegando que toda matéria^[15]^[16] tem uma natureza ondulatória, ele relacionou comprimento de onda e momento:

$\lambda ={\frac {h}{p}}$

Esta é uma generalização da equação de Einstein acima, uma vez que o momento de um fóton é dado por $p={\frac {E}{c}}$ , / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

$onde c é a velocidade da luz no vácuo.$

Em física, uma relação de dispersão expressa a relação existente entre as frequências $�$ e o comprimento de onda $\lambda$ , ou, de forma equivalente,^[1] entre as frequências $�$ e as velocidades $�$ , atrelada a entes físicos de natureza ondulatória (fases) propagando-se em um dado meio material ou mesmo no vácuo. Geralmente, traduz-se mediante uma função ou um gráfico de frequência x comprimento de onda — ou de frequência x velocidade — e quase sempre mostra-se bem dependente do meio de propagação, caracterizando-o inclusive.

De forma similar mas não idêntica, um espectro discrimina a amplitude ou intensidade — o que se traduz, geralmente, por quantidade de energia — das fases como função de suas respectivas frequências. Espectros e relações de dispersão encontram-se certamente relacionados, mas são por definição distintos.

Óptica

A relação de dispersão influi diretamente nas trajetórias de propagação de ondas quando há mudança do meio de propagação, visto que as relações de dispersão são, geralmente, diferentes nos diferentes meios de propagação e que as mudanças nas direções de propagação ocorrem, justamente, em virtude de mudanças nos comprimentos de onda quando ondas com uma dada frequência atravessam a interface entre os diferentes meios. A dependência dessas variações nas direções de propagação com a as frequências ou comprimentos de onda explicam porque a luz branca é, por meio de um fenômeno óptico conhecido por refração, separada em suas várias cores (frequências) ao atravessar um prisma ou mesmo gotas de água. As relações de dispersão para a onda no ar e no vidro, ou no ar e na água, são bem distintas: em ambos os casos as componentes das ondas são fisicamente separadas em função de suas frequências, cada qual sofrendo um maior ou menor desvio em sua trajetória ao mudarem de meio, o que dá origem, por fim, aos espectros e ao arco-iris.

A relação de dispersão é importante para entender como que a energia, o momento ou mesmo a matéria são transportados de um ponto a outro em qualquer meio. O interesse na relação de dispersão provavelmente começou com o interesse na dispersão de ondas na água, como, por exemplo, demostrado por Pierre-Simon Laplace em 1776.^[2]

Mecânica

Em mecânica, o termo relação de dispersão refere-se à relação — normalmente uma função — que estabelece a energia que um dado ente físico possui em função do momento que este transporta. Em partículas livres, no domínio da física clássica — com massas de repouso não nulas e velocidades muito inferiores à da luz — a relação de dispersão é uma função quadrática do momento: $E={\frac {{\vec {P}}^{2}}{2m}}$ . / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

$E_{c}={\frac {1}{2}}mv^{2}$ / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

${\vec {P}}=m{\vec {V}}$ / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

A relação acima vale no contexto da física clássica e para partículas completamente livres. Em situações mais específicas, como aquelas encontradas em física do estado sólido, a exemplo no estudo de elétrons confinados na estrutura dos cristais semicondutores, a relação de dispersão para as partículas — no caso os elétrons — pode mostrar-se dependente, inclusive, da direção de propagação delas dentro do sistema. O momento para os elétrons dentro dos cristais é definido de forma adequada à situação, sendo então denominado momento cristalino do elétron.

No âmbito da relatividade ou da mecânica quântica, as expressões que definem o momento das partículas em estudo podem assumir formas também bem distintas da expressão clássica ${\vec {P}}=m{\vec {v}}$ , o mesmo ocorrendo para as expressões da energia, mas, em qualquer caso, a relação entre o momento e a energia — ou seja, a relação de dispersão — mostra-se igualmente importante, sendo geralmente o cerne de qualquer teoria que busque estabelecer a dinâmica de matéria, energia e momento nos sistemas físicos sob seu domínio.

Em qualquer teoria dinâmica, a relação de dispersão mostra-se fundamental, e a partir dela é que se definem outras grandezas geralmente importantes ao estudo, como a massa.

A associação do termo "relação de dispersão" com a relação existente entre energia e momento para os entes físicos com massa de repouso (partículas massivas) decorre diretamente dos princípios estabelecidos por De Broglie e Max Planck no âmbito da física quântica. De Broglie trouxe à luz o fato de que partículas massivas têm comportamento ondulatório, e seus comprimentos de onda encontram-se relacionados aos seus momentos, ao passo que, sob a mesma óptica, Plank mostrou que a energias associadas às partículas quânticas encontram-se relacionadas às frequências das ondas a elas associadas. Estabelecer uma relação entre energia e momento é, assim, estabelecer uma relação entre frequência e comprimento de onda, ou seja, estabelecer uma relação de dispersão, mesmo para o caso de partículas massivas.

Relações de dispersão para o vácuo

Fato curioso e de relevância na mecânica quântica é que, ao passo que o vácuo é um meio não dispersivo para ondas eletromagnéticas (as assim chamadas velocidades de fase são iguais à velocidade de grupo em um pulso eletromagnético — todos com velocidades iguais à "c", a velocidade da luz), o vácuo é um meio dispersivo para ondas de matéria (funções de onda), a velocidade de fase dependendo do momento segundo a relação ^[3]:

$V_{\phi }={\frac {\hbar k}{(2m)}}={\frac {p}{2m}}$

$para partículas livres (ondas de matéria planas).$

Repare que a velocidade (real) esperada para a partícula não é a velocidade de fase de uma onda plana de matéria (partícula livre), mas sim a velocidade de grupo das ondas que formam o pacote de ondas associado à partícula, a velocidade de grupo obedecendo relação bem mais similar à esperada classicamente:

$V_{g}={\frac {\hbar k}{m}}={\frac {p}{m}}$

na qual, $\hbar$ é a constante reduzida de Planck, p é o módulo do momento e k o número de onda atrelados à partícula em questão.

• Colisão entre uma carga pontual, mais um núcleo pesado com carga Q=Ze é um projétil leve com carga q=ze é considerada como sendo elástica.

• Momento e energia são conservados.

• As partículas interagem através da força de Coulomb.

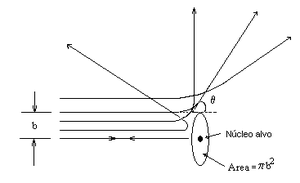
• A distância vertical onde o projétil se encontra a partir do centro do alvo, o parâmetro de impacto b , determinam o ângulo de dispersão θ.

A relação entre o ângulo de dispersão θ, a energia cinética inicial

$E=z{\frac {1}{2}}m.v_{o}^{2}$

e o parâmetro de impacto b é dado pela relação

$b={\frac {zZ}{2K}}.{\frac {e^{2}}{4\pi \varepsilon _{o}}}{\text{cot}}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}$ (1,1) / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

onde z = 2, para partículas-α e Z = 79 de ouro.

Em física, a dispersão de Rutherford é um fenômeno que foi explicado por Ernest Rutherford em 1909,^[1] e levou ao desenvolvimento da teoria orbital do átomo. É agora explorado pela técnica de análise de materiais espectrometria de dispersão de Rutherford. A dispersão de Rutherford é também referida às vezes como dispersão de Coulomb porque baseia-se em forças eletrostáticas (Coulomb). Um processo similar provou o interior do núcleo nos anos 1960, chamado dispersão profunda inelástica.

Principais pressupostos:

• Colisão entre uma carga pontual, mais um núcleo pesado com carga Q=Ze é um projétil leve com carga q=ze é considerada como sendo elástica.

• Momento e energia são conservados.

• As partículas interagem através da força de Coulomb.

• A distância vertical onde o projétil se encontra a partir do centro do alvo, o parâmetro de impacto b , determinam o ângulo de dispersão θ.

A relação entre o ângulo de dispersão θ, a energia cinética inicial

$E=z{\frac {1}{2}}m.v_{o}^{2}$

e o parâmetro de impacto b é dado pela relação

onde z = 2, para partículas-α e Z = 79 de ouro.

Dedução da Transversal Diferencial

Na Figura , uma partícula que atinge o anel entre b e b + db é desviada num ângulo sólido dΩ entre θ e θ + dθ.

Por definição, a secção transversal é a constante de proporcionalidade

$2\pi b.db=-\sigma (\theta ).2\pi .\operatorname {sen} \theta .d\theta$

então

$d\sigma =2\pi b|db|={\Bigg (}{\frac {d\sigma }{d\Omega }}{\Bigg )}.d\Omega$ (1,2) / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

onde $d\Omega =2\pi .\operatorname {sen} \theta .d\theta$

A seção transversal diferencial torna-se então

${\frac {d\sigma }{d\Omega }}={\frac {2\pi b|db|}{2\pi .\operatorname {sen} \theta .d\theta }}$ (1,3) / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

A partir da Equações 1,1 e 1,3 nós temos

${\frac {d\sigma }{d\Omega }}={\Bigg (}{\frac {1}{4\pi \varepsilon _{o}}}{\Bigg )}^{2}{\Bigg (}{\frac {qQ}{4K_{\alpha }}}{\Bigg )}^{2}.{\frac {1}{\operatorname {sen} ^{4}}}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}$ (1.4) / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

A Eq.1.4, é chamada seção transversal diferencial para a dispersão de Rutherford.

Nos cálculos acima, considera-se apenas uma única partícula alfa. Num experimento de dispersão, é preciso considerar vários eventos de dispersão e medir-se a fracção de partículas desviadas num determinado ângulo.

Para um detector em um ângulo específico em relação ao feixe incidente, o número de partículas por unidade de superfície, colidindo o detector, é dado pela fórmula de Rutherford:

$N(\theta )={\frac {N_{i}.nLZ^{2}k^{2}.e^{4}}{4.r^{2}k.E^{2}\operatorname {sen} ^{4}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}}}$

Onde:

Ni = número de partículas alfa incidentes;

n = átomos por unidade de volume no alvo;

L = espessura do alvo;

Z = número atómico do alvo;

e = carga electrónica;

k = constante de Coulomb;

r = distância entre o alvo e o detector;

KE = energia cinética das partículas alfa;

θ = ângulo de dispersão.

A variação prevista, de partículas alfa detectadas, com ângulo é seguida de perto podados do contador de Geiger-Marsden, mostrados na Figura abaixo.

Cálculo do tamanho nuclear máximo

Para colisões frontais cabeças entre partículas alfa e o núcleo, toda a energia cinética $\scriptstyle E=z{\frac {1}{2}}m.v_{o}^{2}$ da partícula alfa é transformada em energia potencial e a partícula está em repouso.

A distância entre o centro da partícula alfa e o centro do núcleo (b) neste momento é um valor máximo para o raio, se é evidente a partir da experiência que as partículas não atingiram o núcleo.

Aplicando a energia potencial de Coulomb entre as cargas nos electrões e no núcleo, pode-se escrever:

${\frac {1}{2}}.m.v^{2}={\frac {1}{4\pi \varepsilon _{o}}}.{\frac {q_{1}q_{2}}{b}}$

Reorganizando,

${\frac {1}{4\pi \varepsilon _{o}}}{\frac {2.q_{1}q_{2}}{m.v^{2}}}$ (1,6) / $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$